Главные и эквивалентные напряжения
Напомним некоторые основные положения теории напряжений, излагаемые обычно в курсе теории упругости или в подробных учебниках сопротивления материалов.
Если выделять из тела в окрестности некой точки (рис. 12.1) элементарный объем в виде бесконечно малого параллелепипеда, то действие на него окружающей среды заменяется напряжениями, компоненты которых действуют на грани параллелепипеда.
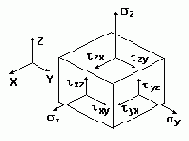
Рис. 12.1
В силу закона парности касательных напряжений



В общем случае в точке имеется только шесть независимых компонент напряжений, которые образуют симметричный тензор напряжений

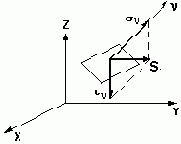
На проходящей через ту же точку произвольно ориентированной площадке, нормаль которой n имеет направляющие косинусы l, m, n с осями x, y, z, действует нормальное напряжение sn
и касательное напряжение tn (рис. 12.2) с равнодействующей Sn. Проекции этой равнодействующей на координатные оси Snx, Sny, Snz связаны с компонентами напряжений условиями равновесия (формула Коши):

Существуют три таких взаимно перпендикулярных площадки, на которых касательные напряжения отсутствуют. На этих, так называемых, главных площадках действуют главные напряжения
s1, s2 и s3. При этом имеется в виду, что s1³s2³s3. Известно также, что главные напряжения обладают экстремальными свойствами, а именно – на любой площадке результирующее напряжение


Направляющие косинусы lk , mk и nk нормалей главных площадок nк определяются из решения системы уравнений:
(sх – sk) lk + txy
mk + txz nk
= 0;
txy lk + (sy – sk) mk + tyz
nk = 0;
txz lk + tyz mk + (sz – sk) nk = 0;
lk2
+ mk2 + nk2 = 1. (12.4)
Из (4) следует, что главные напряжения sk (к=1,2,3) являются корнями кубического уравнения:

Уравнение (5) в развернутой форме имеет вид

а его коэффициенты являются инвариантами (т.е. не зависят от выбора системы координат). Первый инвариант


Направление главных площадок может быть определено не девятью направляющими косинусами, а тремя Эйлеровыми углами:
q – угол (нутации) между положительными направлениями оси Z и n3 (0£q£p);
y – угол (прецессии) между осью X и осью А, идущей вдоль линии пересечения плоскостей XOY и n1Оn2 так, чтобы ОА, Z и n3 образовали правую тройку, при этом угол y увеличивается от оси X к оси Y (0£y£2p);
j – угол (чистого вращения) между осями n1
и А, который увеличивается от n1
к n2 (0£j£2p).
Для характеристики НДС используется коэффициент Лоде-Надаи

принимающий значения m0=1 при чистом сжатии, m0=0 при чистом сдвиге, m0=-1 при чистом растяжении.
В принятых обозначениях при выводе результатов расчета тензор напряжений (2) в общем случае выглядит как

В SCAD главные напряжения


Для углов Эйлера введены обозначения:
q – ТЕТА,
y – PSI,
j – FI.